有限元模态（振型）分析

自然界的物体都有其自己的固有振动频率，例如大型桥梁、摩天大楼和机械结构等，如果外界激励的频率与其固有频率相同或者相近，那么该结构的振动会越来越剧烈，长期受这种激励的作用，势必会使结构损坏。通过模态分析，可以计算结构的固有频率和模态（振型），提高设计质量，例如对于汽车来说，一般不希望第一阶非刚性模态的固有频率不低于某一值，否则就是不合格的设计。

仍以图1所示的某轿车后底板为分析对象，后底板的原始设计厚度T=0.8mm，计算出的前10阶固有频率以及对应的模态（振型）如表1所示。

轿车后底板的模态（振型）
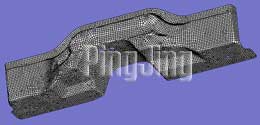
前围板有限元模型
前围板模态（振型）
前围板模态（振型）
前围板模态（振型）

表1 厚度T=0.8mm时的模态

模态	固有频率（Hz）	模态（振型）
1	Frequency=5.52
2	Frequency=6.83
3	Frequency=15.14
4	Frequency=18.52
5	Frequency=24.00
6	Frequency=24.77
7	Frequency=26.32
8	Frequency=29.67
9	Frequency=31.00
10	Frequency=35.60

将后地板的设计厚度改为T＝0.9mm后，后地板的固有频率以及对应的模态（振型）如表2所示。

表1 厚度T=0.9mm时的模态

模态	固有频率（Hz）	模态（振型）
1	Frequency=5.98
2	Frequency=7.24
3	Frequency=16.07
4	Frequency=19.62
5	Frequency=26.20
6	Frequency=26.53
7	Frequency=28.26
8	Frequency=32.70
9	Frequency=33.36
10	Frequency=38.16